Sal performs partial fraction expansion upon (10x²12x)/(x³8) equal to 4 C is equal to 4 and a is equal to 7 so the partial fraction decomposition of this we're now done is 7 over X minus 2 plus 3 X plus 4 over x squared plus 2x plus 4 well that was a pretty tiring problem and you can see the partial fraction decomposition becomes aExpand (x^23y)^3 Desarrollar ecuaciones Symbolab This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Learn more Accept Soluciones Gráficos Practica Geometría betaJointly X and Y take values in the unit square The event 'X > Y ' corresponds to the shaded lowerright triangle below Since the density is constant, the probability is just the fraction of the total area taken up by the event In this case, it is clearly 05

Partial Fraction Expansion Repeated Factors Video Khan Academy
Expand 3 x 2 y 7 square
Expand 3 x 2 y 7 square-In that case −3 5 = 15 (a positive answer), but here is an example where the second part is negative So the second term ended up negative because 2x −a = −2ax, (it is also neater to write "−2ax" rather than "−2xa") That was also interesting because of x being squared (x 2) Lastly, we have an example with three terms insideExpand Master and Build Polynomial Equations Calculator Since (2x 5) 3 is a binomial expansion, we can use the binomial theorem to expand this expression n!




Selina Concise Mathematics Class 8 Icse Solutions Chapter 12 Algebraic Identities Cbse Tuts
X Y Z Whole Square Is Equal To If x 1 p y q z r and xyz then if x 1 p y q z r and xyz then y and z are positive integers such x 3 y z is equal x 3 y z is equal Formula For X Y Z 2 Brainly In Expand Form Of X Y Z Whole Square Brainly In Simplify X Y Z Whole Square Minus Brainly In If X Y Z Is Equal To 10 And Square 40 FindFind the coefficient of x 4 in the expansion of (1 x 3) 50 (x 2 1/x) 5 Solution Solving quadratic equations by completing square Nature of the roots of a quadratic equations Find The Value Of X Cube Y Z Minus 3 If Square Is Equal To Brainly In Using Properties Of Determinants Prove That Y X 2 Xy Zx Z Yz Xz 2xyz 3 Sarthaks Econnect Largest Education Munity X y whole square brainly in prove the idenies z x y 2 4 expand form of x y z whole square brainly in 1 using properties of determinants prove the following x y
So in our case (x y)7 = (7 0)x7 (7 1)x6y (7 6)xy6 (7 7)y7 These ( 7 n) coefficients occur as the 8th row of Pascal's triangle (or 7th if you choose to call the first row the 0th one as some people do)Students trying to do this expansion in their heads tend to mess up the powers But this isn't the time to worry about that square on the xI need to start my answer by plugging the terms and power into the TheoremThe first term in the binomial is "x 2", the second term in "3", and the power n is 6, so, counting from 0 to 6, the Binomial Theorem gives me3) Coefficient of x in expansion of (x 3)5 4) Coefficient of b in expansion of (3 b)4 5) Coefficient of x3y2 in expansion of (x − 3y)5 6) Coefficient of a2 in expansion of (2a 1)5 Find each term described 7) 2nd term in expansion of (y − 2x)4 8) 4th term in expansion of (4y x)4
Click here👆to get an answer to your question ️ Three lines x 2y 3 = 0, x 2y 7 = 0 and 2x y 4 = 0 form the three sides of two squares The equation to the fourth side of each square isThis calculator allows to expand all forms of algebraic expressions online, it also helps to calculate special expansions online (the difference of squares, the identitiy for the square of a sum and the identity for the square of a difference) For simple expansions, theHarnett, ch 3) A The expected value of a random variable is the arithmetic mean of that variable,



Q Tbn And9gcs2zs2yfches1lr N5klpkw0xqulrzmkaw3kumfnpmy Afpiwp Usqp Cau




The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets
Get stepbystep solutions from expert tutors as fast as 1530 minutes Explanation The Binomial Theorem tells us (x y)N = N ∑ n=0(N n)xN −nyn where (N n) = N!Polynomial Identities When we have a sum (difference) of two or three numbers to power of 2 or 3 and we need to remove the brackets we use polynomial identities (short multiplication formulas) (x y) 2 = x 2 2xy y 2 (x y) 2 = x 2 2xy y 2 Example 1 If x = 10, y = 5a (10 5a) 2 = 10 2 2·10·5a (5a) 2 = 100 100a 25a 2
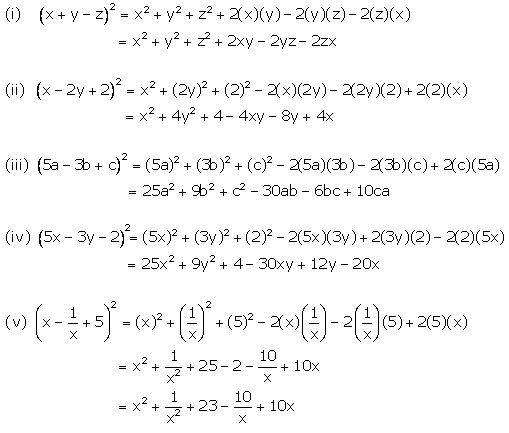



Chapter 4 Expansion Selina Concise Mathematics Part I Solutions For Class 9 Mathematics Icse Topperlearning



Http Mrsk Ca Ap 5 1foil Pdf
Subtract \left (x3\right)^ {2} from 7 Subtract ( x 3) 2 from 7 \left (y6\right)^ {2}=\left (x3\right)^ {2}7 ( y 6) 2 = − ( x 3) 2 7 Take the square root of both sides of the equation Take the square root of both sides of the equation y6=\sqrt {x^ {2}6x2} y6=\sqrt {x^ {2}6x2}4 Binomial Expansions 41 Pascal's riTangle The expansion of (ax)2 is (ax)2 = a2 2axx2 Hence, (ax)3 = (ax)(ax)2 = (ax)(a2 2axx2) = a3 (12)a 2x(21)ax x 3= a3 3a2x3ax2 x urther,F (ax)4 = (ax)(ax)4 = (ax)(a3 3a2x3ax2 x3) = a4 (13)a3x(33)a2x2 (31)ax3 x4 = a4 4a3x6a2x2 4ax3 x4 In general we see that the coe cients of (a x)n75 Least Squares Estimation Version 13 74 Correlation and Regression As must by now be obvious there is a close relationship between correlation and fitting straight lines We define S xx = 1 n X i (x i − x¯)2 S yy = 1 n X i (y i − y¯)2 S xy = 1 n X i (x i − x¯)(y i − y¯) (18) The correlation coefficient r expressing the




Properties Of Determinant Determinant A If A Determinant Of Determinant Example 2 Find The Value Of The Determinant 2 3 1 Example 3 Prove That 1 1 1 Ab Pdf Document




1 Expand And Simplify A 15ab 2ac 4bc B 3x2x Gauthmath
X^ {2}y^ {2}3=0 Subtract 3 from both sides x=\frac {0±\sqrt {0^ {2}4\left (y^ {2}3\right)}} {2} This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 0 for b, and y^ {2}3 for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a} x=\frac {0±\sqrt {4\left (y^ {2}3\right)}} {2}Expectations Expectations (See also Hays, Appendix B;Expand ln(x2) ln ( x 2) by moving 2 2 outside the logarithm Expand ln(y3) ln ( y 3) by moving 3 3 outside the logarithm Multiply 3 3 by −1 1 Apply the distributive property Cancel the common factor of 2 2 Tap for more steps Factor 2 2 out of 2 ln ( x) 2 ln ( x) Cancel the common factor



2




If In The Expansion Of 1 X 15 The Coefficients Of 2r 3
This occurs for K = 7, 15, and 115, so the nonnegative integers K such that every positive integer N of the form (x^2 Kxy y^2)/(1xy) greater than K is a square is 0, 1, 3, 4, 5, 7, 15, 115 The number of minimal pairs x,y with opposite sign yielding integer values of N tends to increase as K increases, but it appears that there are infinitely many K for which the only reduced pair is 1,2Solve the following simultaneous equations algebraically 6 y= x3, y=2x^2 8x 7 This question is asking you to solve, therefore you need to show detailed working out in logical steps to show the examiner how you reach your solution To solve simultaneous equations we first need to eliminate one of the variables, either x or y In this(x y) 7 = x 7 7x 6 y 21x 5 y 2 35x 4 y 3 35x 3 y 4 21x 2 y 5 7xy 6 y 7 When the terms of the binomial have coefficient(s), be sure to apply the exponents to these coefficients Example Write out the expansion of (2x 3y) 4




Simplify Simplify Radical Rational Expression With Step By Step Math Problem Solver




Form 2 Unit 2 Lesson 6 Multiplying Two Binomials Brilliant Maths
−3a 2(3−b) = −9a 23a b Example Expand (x5)x Here, the brackets appear first, but the principle is the same Both terms inside must be multiplied by the x outside (x5)x = x 5x Exercises 1 Remove the brackets from the following expressions a) 5(x4) b) 2(y −3) c) 4(3− a) d) x(2x) e) p(q 3) f) −3(2a) g) s(t− s) h) −2(bSlope y= 3/ (sqrt (x)) \square!In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial According to the theorem, it is possible to expand the polynomial n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with b c = n, and the coefficient a of each term is a specific positive integer depending on n and b For example, 4 = x 4 4 x 3 y 6 x 2 y 2 4 x y 3 y 4 {\displaystyle ^{4}=x^{4}4x^{3}y6x^{2}y^{2}4xy^{3}y



Cbse 9 Math Cbse Polynomials Ncert Solutions




Videos And Worksheets Corbettmaths
Expand And Factorize Quadratic Expressions Expanding Quadratic Expressions Quadratic expressions are algebraic expressions where the variable has an exponent of 2 For example x 2 3x 4 To expand quadratic equations, use the FOIL (First, Outside, Inside, Last) methodThey have the sameIf x x x and y y y are real numbers such that x y = 7 xy=7 x y = 7 and x 3 y 3 = 133 x^3y^3=133 x 3 y 3 = 1 3 3, find the value of x y xy x y Submit your answer 3 3 ( 1640 ) 1 3 \sqrt{\sqrt{\sqrt3{\color{#3D99F6}{}} {\sqrt3{\color{#3D99F6}{} \color{teal}{3(1640) 1}}}}} 3 6 4 0 0 0 3 6 4 0 0 0 3 ( 1 6 4 0 ) 1




Pdf G3z3002 Minitest Bash Bash Academia Edu




Partial Fraction Expansion Repeated Factors Video Khan Academy
Find the value of (i) coefficient of x 3 (ii) coefficient of x 2 Find the term involving x^2 in the expansion of (x^3k/x)^10 Pinoybixorg is an engineering education website maintained and designed toward helping engineering students achieved their ultimate goal to become a fullpledged engineers very soonExpand and Simplify (i) 2(x 4) 3(x 2) (ii) x(x 3) (iii) y(2y 3) (iv) (x 3)(x 4) (v) (x 3)(x 9)




Expand 3x 7y Z 2 Using Identities Brainly In




X 2 3 Expand Novocom Top
The number x is 2 more than the number y If the sum of the squares of x and y is 34, then find the product of x and y Solution 15 Given x is 2 more than y, so x = y 2 In the expansion of (2x 2 8) (x 4) 2;17 Factorisation (EMAG) Factorisation is the opposite process of expanding brackets For example, expanding brackets would require \ (2 (x 1)\) to be written as \ (2x 2\) Factorisation would be to start with \ (2x 2\) and end up with \ (2 (x 1)\) The two expressions \ (2 (x 1)\) and \ (2x2\) are equivalent; To identify the least squares line from summary statistics Estimate the slope parameter, b 1, using Equation 734 Noting that the point ( x ¯, y ¯) is on the least squares line, use x 0 = x ¯ and y 0 = y ¯ along with the slope b 1 in the pointslope equation (737) y − y ¯ = b 1 ( x − x ¯) Simplify the equation




Pls Solve It Fast 5 6 8 9 14 15 Expand Use Appropriate Formulae Maths Meritnation Com




Powers In Brackets How To Use The Bracket Power Rule Owlcation
In other words, a number y whose square (the result of multiplying the number by itself, or y ⋅ y) is x For example, 4 and −4 are square roots of 16, because 42 = (−4)2 = 16 Every nonnegative real number x has a unique nonnegative square root, called the principal square root, which is denoted by x, {\displaystyle {\sqrt {xMultiply both sides of the equation by (1) to obtain positive coefficient for the first term x29x7 = 0 Subtract 7 from both side of the equation x29x = 7 Now the clever bit Take the coefficient of x , which is 9 , divide by two, giving 9/2 , and finally square itFactorising an expression is to write it as a product of its factors There are 4 methods common factor, difference of two squares, trinomial/quadratic expression and completing the square




Expand Using Identity 3 X Minus 2 Y Z Whole Square Brainly In




Core 1 Revision Sheet
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorThe difference of two squares means one squared term subtract another squared term For example, \(x^2 9\) would be the difference of two squares as \(x^2\) is a squared term (\(xAnswer (−2x5y−3z)2 is of the form (abc)2 (abc)2 = a2 b2 c2 2ab2bc2ca where a = −2x,b = 5y,c =−3z ∴ (−2x5y−3z)2 = (−2x)2 (5y)2 (−3z)2 2(−2x)(5y)2(5y)(−3z)2
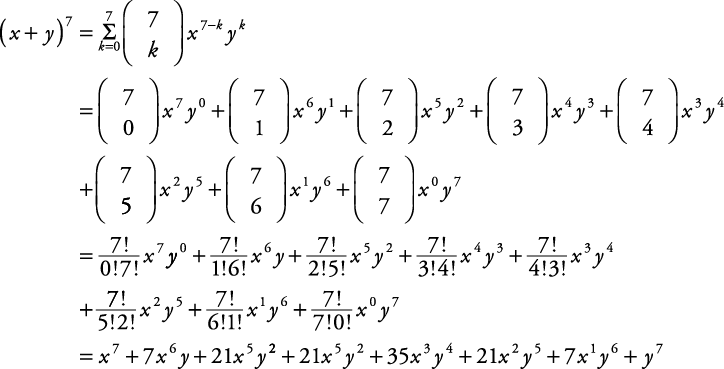



Binomial Coefficients And The Binomial Theorem
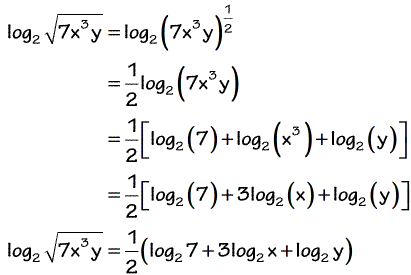



Expanding Logarithms Chilimath
In mathematics, a square root of a number x is a number y such that y2 = x;Divide both sides of the equation by 2 to have 1 as the coefficient of the first term x2 (3/2)x (7/2) = 0 Add 7/2 to both side of the equation x2 (3/2)x = 7/2 Now the clever bit Take the coefficient of x , which is 3/2 , divide by two, giving 3/4 , and finally square it giving 9/16The following are algebraix expansion formulae of selected polynomials Square of summation (x y) 2 = x 2 2xy y 2 Square of difference (x y) 2 = x 2 2xy y 2 Difference of squares x 2 y 2 = (x y) (x y) Cube of summation (x y) 3 = x 3 3x 2 y 3xy 2 y 3 Summation of two cubes x 3 y 3 = (x y) (x 2 xy y 2) Cube of difference (x y) 3 = x 3 3x 2 y 3xy 2 y 3




Simplifying Square Root Expressions Video Khan Academy




Expand And Simplify Gcse Maths Lesson Examples Worksheet
In this case, n = 3, x = 2x, a = 1, and y = 5 Expanding terms, we get Exercise 3 Expand the following expression, writing your answer in its simplest form Be careful of notation and do not use spaces in your answer ( x ) 2 = x2 x >Expand (x 2 3) 6;




Use Identity And Expand 3x 2y 7 2 Brainly In



2
The calculator helps expand and simplify expression online, to achieve this, the calculator combines simplify calculator and expand calculator functions It is for example possible to expand and simplify the following expression ( 3 x 1) ( 2 x 4), using the syntax The expression in its expanded form and reduced 4 14 ⋅ x 6 ⋅ x 2 beChecklist Ready to be marked ?The distributive property is the rule that relates addition and multiplication Specifically, it states that a ( b c) = a b a c a (bc) = ab ac a(bc) = abac ( a b) c = a c b c (ab)c = ac bc (ab)c = acbc It is a useful tool for expanding expressions,




Exponent Rules 7 Key Strategies To Solve Tough Equations Prodigy Education




Find The Coefficient Of X 2 Y 3 Z 4 In The Expansion Of Ax By
X3 = ⋯ = 577 408 = And one can quickly check that (x3)2 = , which is pretty much the square root of 2 We want to (manually) approximate √2 by using the first few terms of the binomial series expansion of √1 − 2x = ∞ ∑ n = 0(1 2 n)( − 2x)n x < 1 2 = 1 − x − 1 2x2 − 1 2x3 ⋯ Here we look for




Expand 3 X 2 Y 7 Square Novocom Top




Factor Factor A Polynomial And Trinomial With Step By Step Math Problem Solver



Corbettmaths Files Wordpress Com 13 02 Expanding Brackets Pdf1 Pdf




Selina Concise Mathematics Class 8 Icse Solutions Chapter 12 Algebraic Identities Cbse Tuts




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes
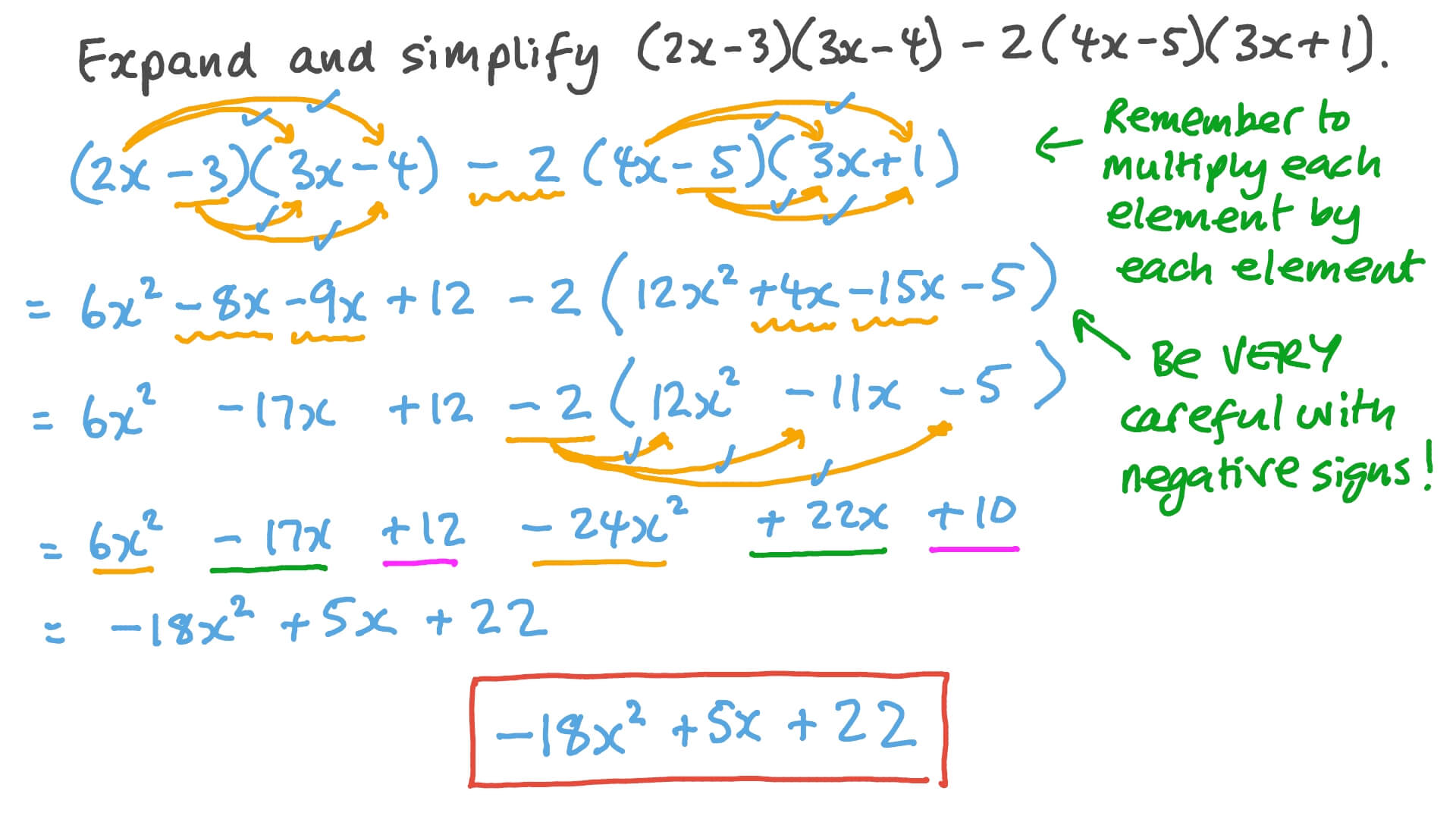



Question Video Expanding And Simplifying Algebraic Expressions Nagwa




What Is The Third Term Of The Binomial Expansion Math 2x Y 6 Math Quora
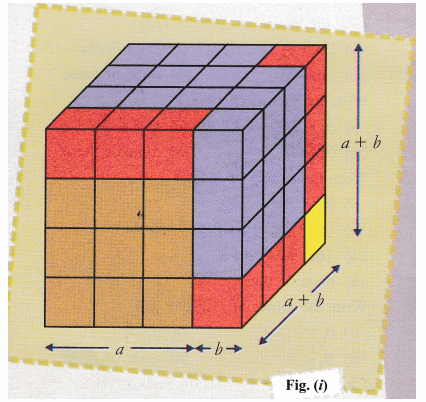



Cbse Class 9 Maths Lab Manual Algebraic Identity A B 3 A3 3a2b 3ab2 Cbse Sample Papers




Ex 8 2 5 Find 4th Term Of X 2y 12 Chapter 8 Class 11




Ex 2 5 4 Expand Each Of The Following Using Suitable



Cbse 9 Math Cbse Polynomials Ncert Solutions



Search Q Binomial Expansion Formula Tbm Isch




Expanding Double Brackets Teaching Resources



Madasmaths Com Archive Maths Booklets Standard Topics Various Binomial Series Expansions Exam Questions Pdf




Factoring Calculator Wolfram Alpha




Expand And Simplify Gcse Maths Lesson Examples Worksheet




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf



1




Forming Polynomial Equations With Roots Video Lesson Transcript Study Com




Maclaurin Expansion For 1 Sqrt X 2 9 Mathematics Stack Exchange




9 Binomial Theorem Example 4 Expanding 3 Terms In A Binomial Question Youtube




Algebra Ppt Download




Expansions Popular Questions Icse Class 9 Math Mathematics Meritnation




Binomial Theorem Wikipedia




If The Coefficient Of X 7 X 8 In The Expansion Of 2 X3 N Are Equal Then The Value Of N Is




Maharashtra Board Class 7 Maths Solutions Chapter 14 Algebraic Formulae Expansion Of Squares Practice Set 50 Learn Cram



Www Jstor Org Stable
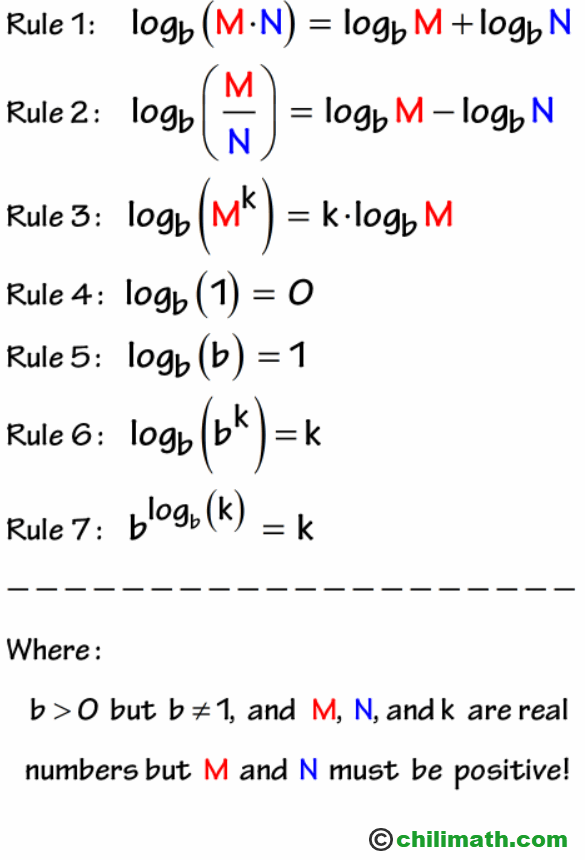



Expanding Logarithms Chilimath




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9



Http Mrsk Ca Ap 5 2specialproductsexpand Pdf
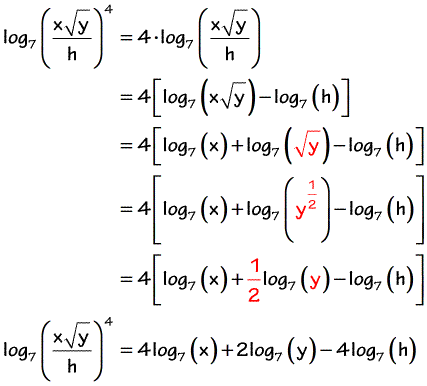



Expanding Logarithms Chilimath



Www Jstor Org Stable




Binomial Theorem Wikipedia



Madasmaths Com Archive Maths Booklets Standard Topics Various Binomial Series Expansions Exam Questions Pdf
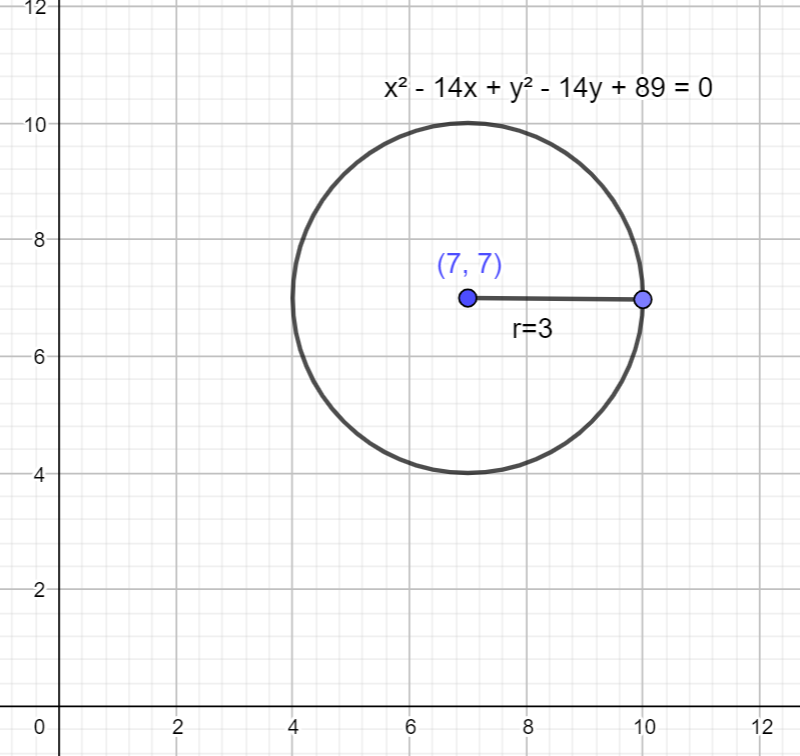



How Do You Graph X214x Y214y 0 Class 11 Maths Cbse




Ppt College Algebra Powerpoint Presentation Free Download Id



The Substitution Method



4 The Binomial Theorem




What Is The Third Term Of The Binomial Expansion Math 2x Y 6 Math Quora
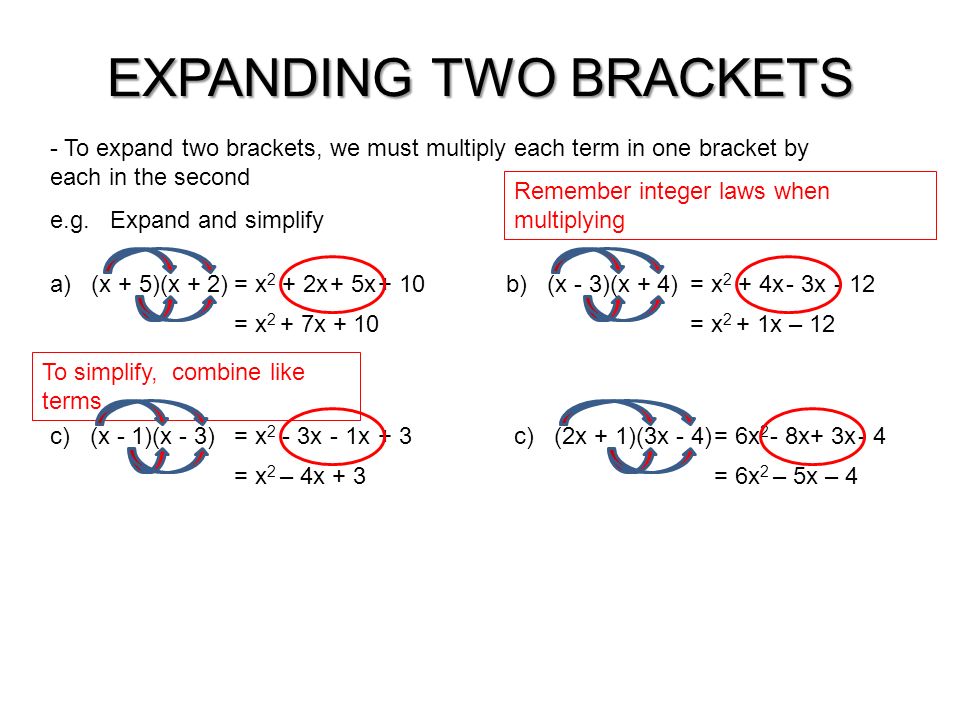



Algebra Ppt Download




Form 2 Unit 2 Lesson 6 Multiplying Two Binomials Brilliant Maths




If A R Is The Coefficient Of X R In The Expansion Of 1 X X 2 N Then A 1 2a 2 3a 3 2na 2n



Surds Mathematics Gcse Revision




Appendex




Expand And Simplify Binomial Squares 2x 3y 2 Youtube




If The Rth Term In The Expansion Of X 3 2 X 2 10 Contains X 4 Then R Is Equal To
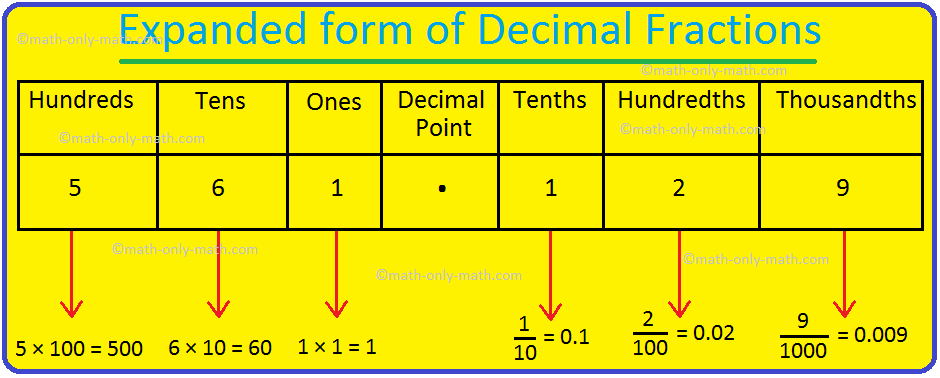



Expanded Form Of Decimal Fractions How To Write A Decimal In Expanded



A Highly Homogeneous Polymer Composed Of Tetrahedron Like Monomers For High Isotropy Expansion Microscopy Nature Nanotechnology
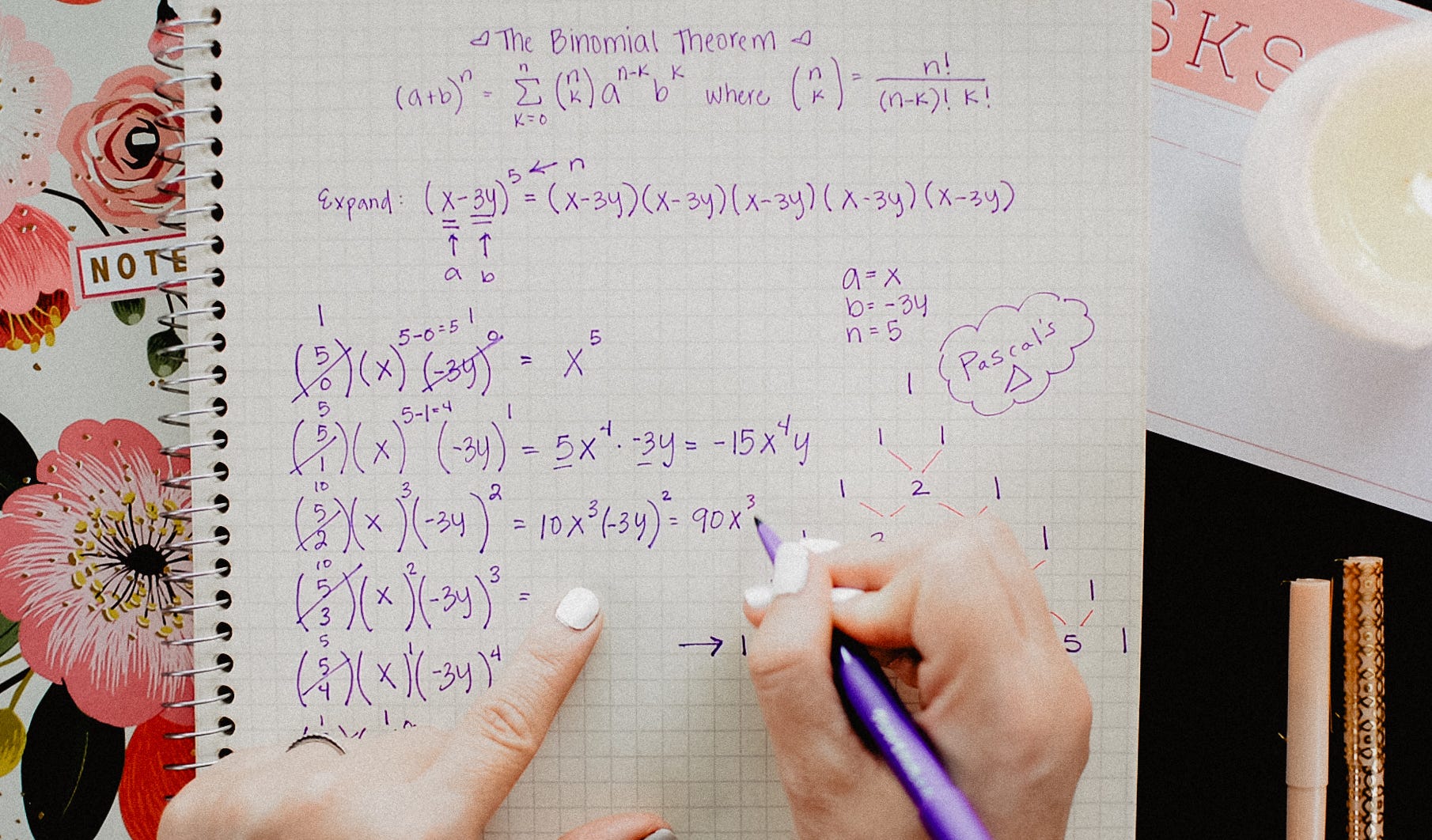



The Binomial Theorem Explained With A Special Splash Of Pascal S By Brett Berry Math Hacks Medium




1 Find The Constant Term In The Expansion Of 1 7x Chegg Com



Http Www Stat Wisc Edu Ifischer Calculus Pdf




Ex 2 5 4 Expand Each Of The Following Using Suitable



1



Www Quia Com Files Quia Users Rsamis Mathpower 9 Chapter 5




Graph Graph Equations And Equation Systems With Step By Step Math Problem Solver




General And Middle Term Binomial Theorem Formula Videos Examples




How To Expand And Simplify X 2 X 3 Quora




9 5 The Binomial Theorem Let S Look At The Expansion Of X Y N Ppt Video Online Download




Expand 3 X 4 Y 5 Z Whole Square Brainly In



4 The Binomial Theorem



2 Use Tkinter To Draw Onto A 500x500 Window Canvas Centered In The Middle Of The Window Draw A Black Empty Square Of Size 300x300 And A Blue Empty Course Hero




Cube Algebra Wikipedia




Coordinate Geometry
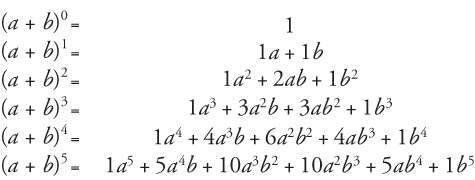



Binomial Coefficients And The Binomial Theorem




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes
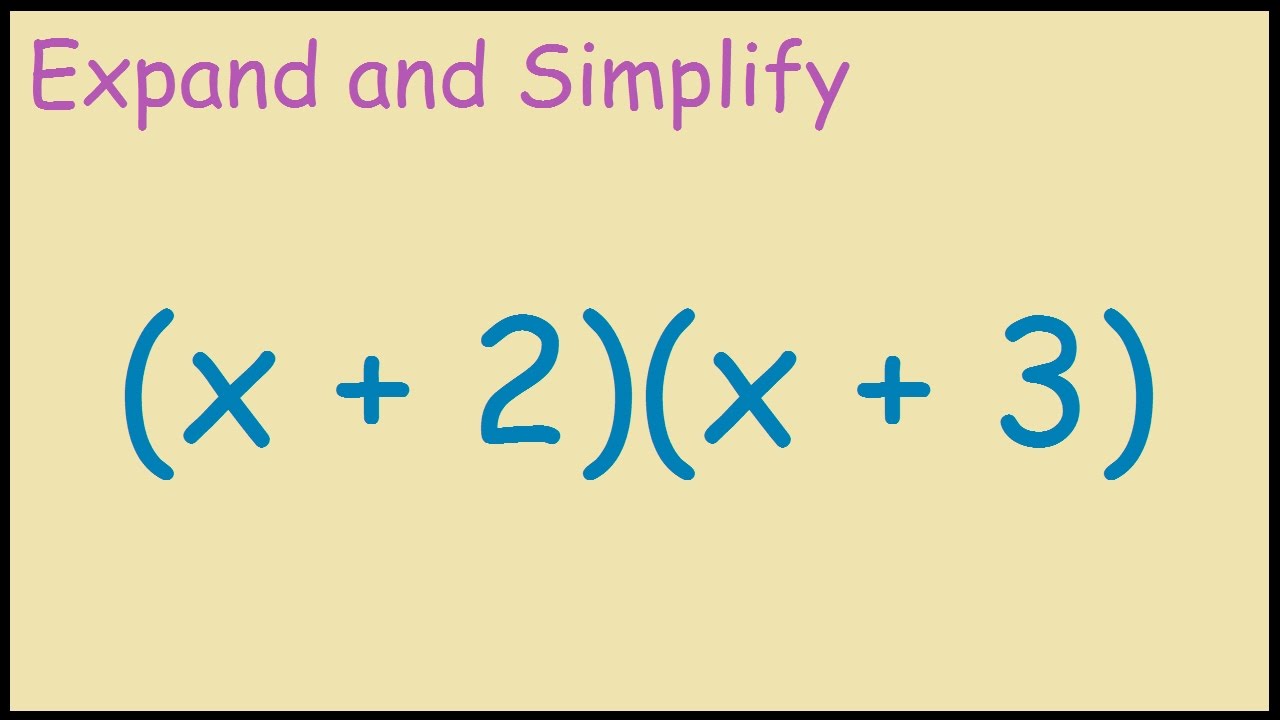



X 2 X 3 Expand And Simplify Youtube



The Substitution Method




3 Binomial Theorem Example 1 A Basic Binomial Expansion Question To Get Used To The Formula Youtube




Ex 8 2 5 Find 4th Term Of X 2y 12 Chapter 8 Class 11




Algebra Ppt Download




Expanding Binomials Video Polynomials Khan Academy




Expanded Notation Video Lessons Examples Solutions




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9



Expand X Y 7 X 2 6 A 2 2b 5 Find The Chegg Com
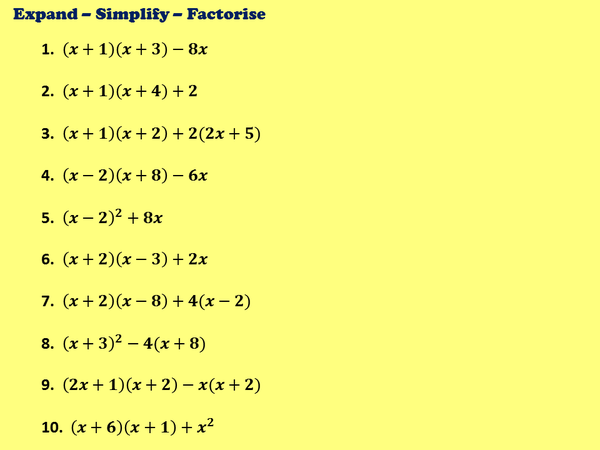



Resourceaholic Algebra



Cbse 9 Math Cbse Polynomials Ncert Solutions



0 件のコメント:
コメントを投稿